
For example, using the default alpha-level of 0.05, Minitab displays a 90% confidence interval. The confidence level for this interval is set at (1 – 2 alpha) x 100%. (1 – 2 alpha) x 100% confidence interval If you change the Options settings to use a (1–2 alpha) x 100% confidence interval for an equivalence test, Minitab displays a (1–2 alpha) x 100% confidence interval. Because the confidence interval incorporates this additional information, a (1 – alpha) x 100% confidence interval for equivalence is in most cases tighter than a standard (1 – alpha) x 100% confidence interval that is calculated for a t-test. For this reason, the confidence interval for equivalence also considers the additional information of the lower and upper limits of the equivalence interval. However, the (1 – alpha) x 100% confidence interval for equivalence is specifically derived to closely correspond with the results of an alpha-level equivalence test.

Like a standard confidence interval, the confidence interval for equivalence is calculated using information about the point estimate of the difference (or ratio), the sample size, and the variability in the data. In these results, using the default (1 – alpha) x 100% method and an alpha of 0.05 produces a 95% CI for equivalence of (0, 2.1928). These equations come from page 217-218 of Sheskin ( Handbook of Parametric and Nonparametric Statistical Procedures, Fifth Edition).Difference SE Equivalence Equivalence IntervalĬI is not within the equivalence interval. N is sample size alpha is 0.05 for 95% confidence, 0.01 for 99% confidence, etc.: These Excel equations compute the confidence interval of a SD. Computing the CI of a Standard Deviation with Excel With small samples, this asymmetry is quite noticeable. This means that the upper confidence interval usually extends further above the sample SD than the lower limit extends below the sample SD. Why? Since the SD is always a positive number, the lower confidence limit can't be less than zero. Note that the confidence intervals are not symmetrical. Random sampling can have a huge impact with small data sets, resulting in a calculated standard deviation quite far from the true population standard deviation. Most people are surprised that small samples define the SD so poorly. When you compute a SD from only five values, the upper 95% confidence limit for the SD is almost five times the lower limit. From the n=5 row of the table, the 95% confidence interval extends from 0.60 times the SD to 2.87 times the SD. But the true standard deviation of the population from which the values were sampled might be quite different. The sample standard deviation computed from the five values shown in the graph above is 18.0. With small samples, the interval is quite wide as shown in the table below. How wide is the CI of the SD? Of course, the answer depends on sample size (N). If you assume that your data were randomly and independently sampled from a Gaussian distribution, you can be 95% sure that the CI computed from the sample SD contains the true population SD. Interpreting the CI of the SD is straightforward.
#Confidence interval minitab free
A free GraphPad QuickCalc does the work for you. It's not done often, but it is certainly possible to compute a CI for a SD.
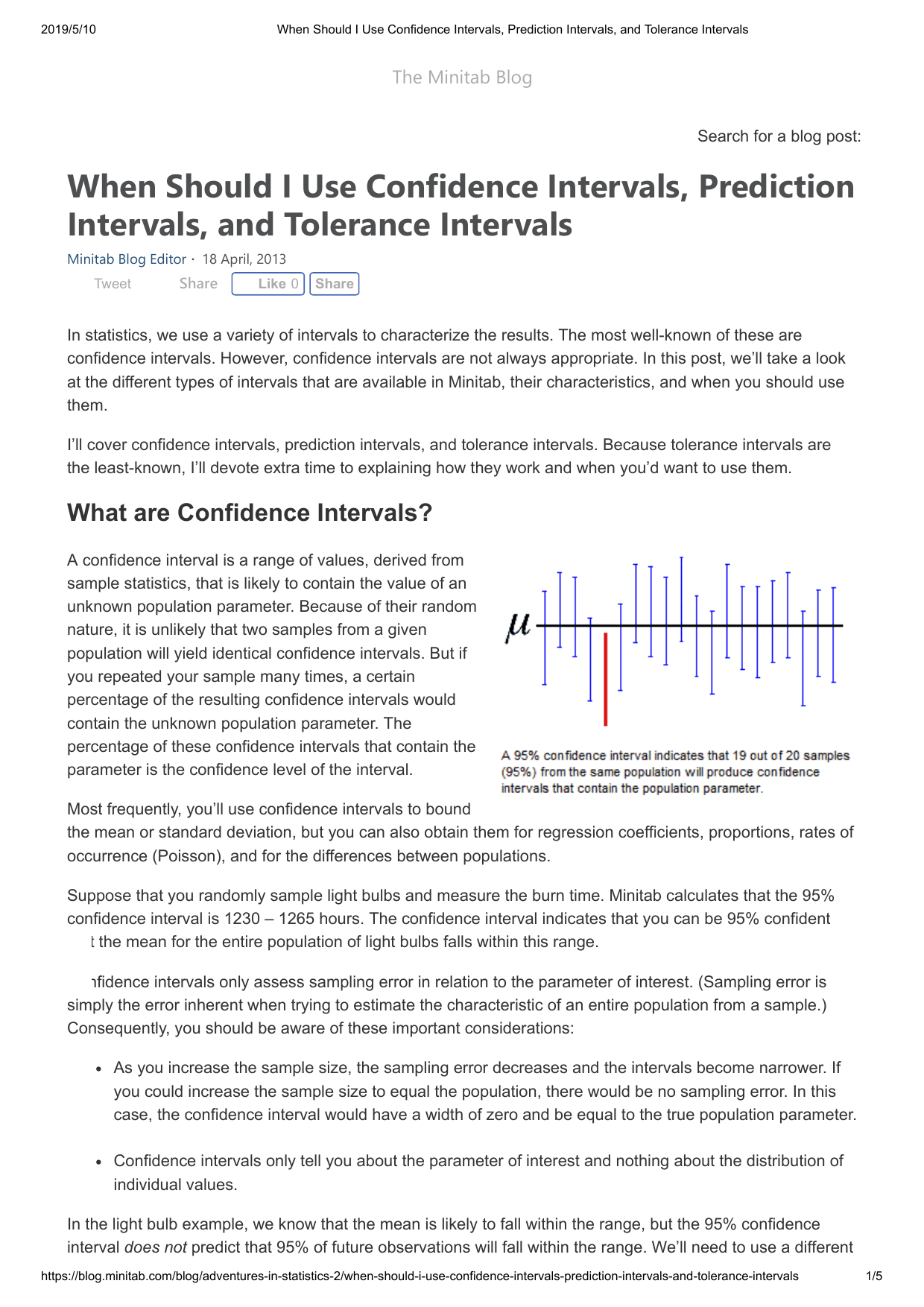
The sample SD is just a value you compute from a sample of data. Another example is a confidence interval of a best-fit value from regression, for example, a confidence interval of a slope. The idea of a confidence interval is very general, and you can express the precision of any computed value as a 95% confidence interval (CI). You are probably already familiar with a confidence interval of a mean. The SD of your sample does not equal, and may be quite far from, the SD of the population. Or you may have randomly obtained values that are far more scattered than the overall population, making the SD high. But how accurate is that standard deviation? Just by chance, you may have happened to obtain data that are closely bunched together, making the SD low.

It is straightforward to calculate the standard deviation from a sample of values. The Standard Deviation of a sample is not the same as the Standard Deviation of the population A confidence interval can be computed for almost any value computed from a sample of data, including the standard deviation (SD).


 0 kommentar(er)
0 kommentar(er)
